Wie finde ich die Regressionsgleichung in Excel?
Wenn Sie auf der Suche nach einer einfachen Möglichkeit sind, die Regressionsgleichung in Excel zu berechnen, sind Sie am richtigen Ort gekommen. In diesem Artikel zeigen wir Ihnen Schritt für Schritt, wie die integrierten Funktionen von Excel die Regressionsgleichung für alle Datenmengen schnell und genau finden. Wir werden erklären, was die Regressionsgleichung ist, wie man sie interpretiert und wie Sie sie verwenden können, um Beziehungen zwischen zwei Variablen zu analysieren. Am Ende dieses Artikels haben Sie ein umfassendes Verständnis dafür, wie die Regressionsgleichung in Excel findet. Also fangen wir an!
Um die Regressionsgleichung in Excel zu finden, müssen Sie folgende Schritte befolgen:
- Öffnen Sie den Datensatz in Excel und wählen Sie die beiden Datenspalten aus, die Sie analysieren möchten.
- Gehen Sie zur Registerkarte Daten und wählen Sie Datenanalyse aus der Analysegruppe.
- Wählen Sie aus der Liste der Analysetools Regression aus und klicken Sie auf OK.
- Wählen Sie die beiden Datenspalten für das Regressionsdialogfeld aus und klicken Sie dann auf OK.
- Die Regressionsgleichung wird im Ausgangsbereich Box angezeigt.
Einführung in die Regressionsgleichung in Excel
Eine Regressionsgleichung ist ein mathematischer Ausdruck, der verwendet wird, um den Wert einer abhängigen Variablen (y) auf der Grundlage des Werts einer unabhängigen Variablen (x) vorherzusagen. In Excel werden Regressionsgleichungen verwendet, um eine lineare Regressionsanalyse durchzuführen. Diese Art der Analyse wird verwendet, um die Beziehung zwischen zwei Variablen zu bestimmen - der abhängigen Variablen und der unabhängigen Variablen. Die Regressionsgleichung hilft, die Stärke der Beziehung zwischen den beiden Variablen zu identifizieren und den Wert der abhängigen Variablen basierend auf dem Wert der unabhängigen Variablen vorherzusagen.
Die Regressionsanalyse ist ein leistungsstarkes Instrument zur Datenanalyse und -prognose. Es kann verwendet werden, um Trends in Daten zu identifizieren, zukünftige Werte vorherzusagen und die am besten geeignete Art der Regressionsgleichung für einen bestimmten Datensatz zu bestimmen. In Excel ist es möglich, eine Regressionsgleichung mit dem Regressionsanalyse -Tool zu erstellen.
Schritte, um die Regressionsgleichung in Excel zu finden
Der erste Schritt, um die Regressionsgleichung in Excel zu finden, besteht darin, den Datensatz auszuwählen, der für die Regressionsanalyse verwendet wird. Der Datensatz sollte zwei Datenspalten enthalten - eine Spalte für die abhängige Variable und eine Spalte für die unabhängige Variable. Sobald der Datensatz ausgewählt wurde, ist es wichtig sicherzustellen, dass die Daten korrekt formatiert sind.
Der nächste Schritt besteht darin, in Excel auf das Tool zur Regressionsanalyse zuzugreifen. Dies kann durch Auswahl der Registerkarte Daten in der Felibbon erfolgen und dann die Option Datenanalyse aus der Analysegruppe auswählen. Sobald das Dialogfeld der Datenanalyse geöffnet ist, sollte die Regressionsoption ausgewählt und die Schaltfläche OK geklickt werden.
Eingabe der Daten in das Regressionstool eingeben
Sobald das Tool zur Regressionsanalyse geöffnet wurde, müssen die Daten für die Regressionsanalyse in das Tool eingegeben werden. Dies kann durch Auswahl der Eingabebereichoption und dann des Datenbereichs durchgeführt werden, der für die Regressionsanalyse verwendet wird. Es ist wichtig sicherzustellen, dass die Daten korrekt formatiert sind, bevor sie in das Tool zur Regressionsanalyse eingegeben werden.
Der nächste Schritt besteht darin, die Option Ausgangsbereich auszuwählen und dann eine Zelle oder einen Zellbereich auszuwählen, in dem die Ausgabe aus der Regressionsanalyse angezeigt wird. Sobald diese Schritte ausgeschlossen sind, sollte die Schaltfläche OK angeklickt werden, um die Regressionsanalyse zu beginnen.
Interpretation der Ausgabe der Regressionsanalyse
Sobald die Regressionsanalyse abgeschlossen ist, wird die Ausgabe der Analyse im ausgewählten Ausgangsbereich angezeigt. Die Ausgabe der Analyse umfasst die Regressionsgleichung, den Bestimmungskoeffizienten (R2) und die F-Statistik. Die Regressionsgleichung ist der mathematische Ausdruck, mit dem der Wert der abhängigen Variablen auf der Grundlage des Werts der unabhängigen Variablen vorhergesagt wird.
Der Bestimmungskoeffizient (R2) ist ein Maß für die Stärke der Beziehung zwischen den beiden Variablen. Die F-Statistik wird verwendet, um festzustellen, ob die Regressionsgleichung statistisch signifikant ist. Wenn die F-Statistik signifikant ist, kann die Regressionsgleichung verwendet werden, um Vorhersagen über den Wert der abhängigen Variablen zu treffen.
Testen der Genauigkeit der Regressionsgleichung
Die Genauigkeit der Regressionsgleichung kann getestet werden, indem die vorhergesagten Werte mit den tatsächlichen Werten im Datensatz verglichen werden. Dies kann durch Auswahl einer neuen Spalte im Datensatz und der Eingabe der Formel für die Regressionsgleichung erfolgen. Die vorhergesagten Werte können dann mit den tatsächlichen Werten verglichen werden, um die Genauigkeit der Regressionsgleichung zu bestimmen.
Verwenden der Regressionsgleichung, um Vorhersagen zu treffen
Sobald die Genauigkeit der Regressionsgleichung getestet wurde, kann sie verwendet werden, um Vorhersagen zu treffen. Dies kann durch Eingeben des Werts der unabhängigen Variablen in die Regressionsgleichung und dann durch Berechnung des vorhergesagten Werts der abhängigen Variablen erfolgen. Dieser vorhergesagte Wert kann dann für die Prognose oder andere Analyse verwendet werden.
Verwenden der Regressionsgleichung, um Trends zu identifizieren
Zusätzlich zur Vorhersage kann die Regressionsgleichung auch verwendet werden, um Trends in den Daten zu identifizieren. Dies kann durch Auftragen der Regressionsgleichung in einem Diagramm und anschließender Analyse der Trends in den Daten erfolgen. Es ist wichtig zu beachten, dass die Regressionsgleichung nur verwendet werden sollte, um Trends in den Daten zu identifizieren und keine Vorhersagen über zukünftige Werte zu treffen.
Nur wenige häufig gestellte Fragen
Was ist eine Regressionsgleichung?
Eine Regressionsgleichung ist ein mathematisches Modell, das die lineare Beziehung zwischen einer unabhängigen Variablen (x) und einer abhängigen Variablen (Y) beschreibt. Die Gleichung wird verwendet, um den Wert der abhängigen Variablen vorherzusagen, wenn der Wert der unabhängigen Variablen bekannt ist.
Was ist die Regressionsgleichungsformel?
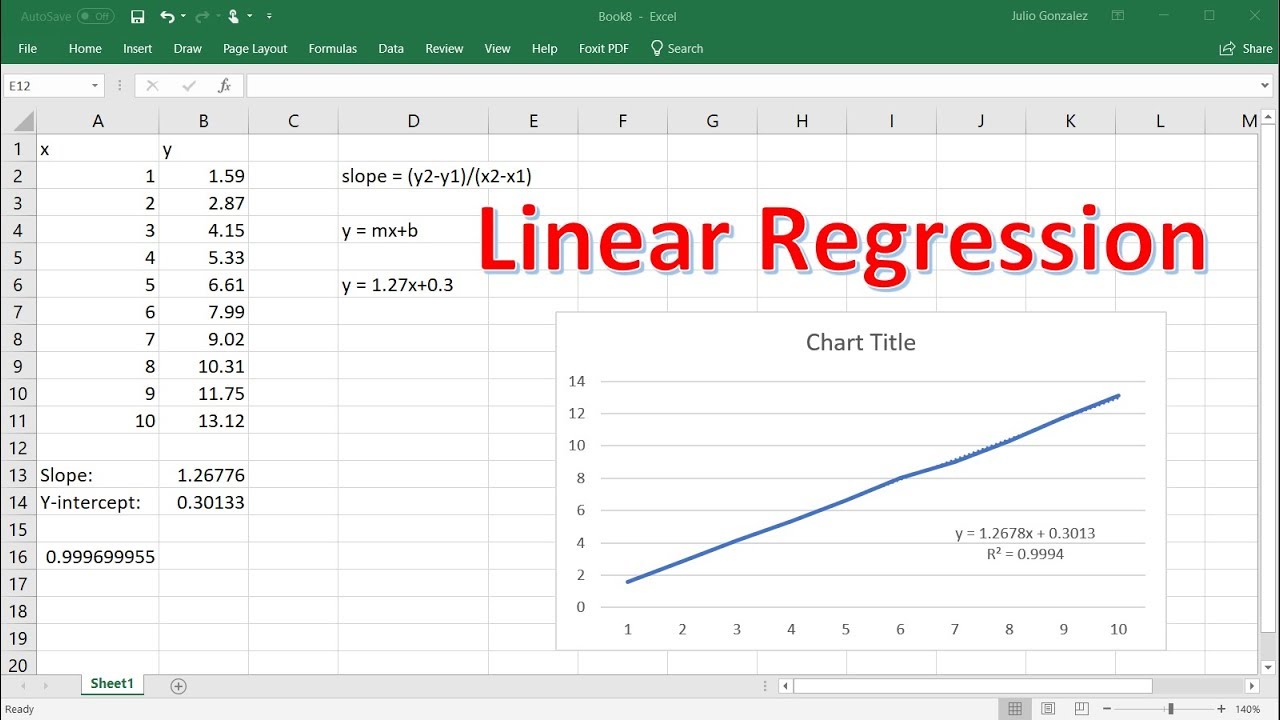
Die Regressionsgleichungsformel ist y = mx + b, wobei m die Steigung der Linie und B der y-Schnittpunkt ist. Die Steigung der Linie ist die Menge, die die abhängige Variable für jede Einheiterhöhung der unabhängigen Variablen ändert. Der y-Schnittpunkt ist der Punkt, an dem die Linie die y-Achse überschreitet.
Wie finde ich die Regressionsgleichung in Excel?
In Excel kann die Regressionsgleichung unter Verwendung der Linest -Funktion gefunden werden. Diese Funktion nimmt zwei Datensätze an, berechnet die Regressionsgleichung und gibt die Steigung und den Y-Grenzübernahme der Gleichung zurück. Um die Linest -Funktion zu verwenden, müssen die Daten in Spalten organisiert werden. Die unabhängige Variable wird in einer Spalte platziert und die abhängige Variable in einer anderen Spalte platziert. Anschließend wird die Linest -Funktion mit den beiden Spalten als Argumente eingegeben.
Was ist die Syntax für die Linest -Funktion in Excel?
Die Syntax für die Linest -Funktion in Excel ist = linest (bekannte_ys,
Was ist R-Quadrat?
R-Quadrat ist ein statistisches Maß dafür, wie gut die Regressionsgleichung den Daten passt. Es wird berechnet, indem das Quadrat des Korrelationskoeffizienten eingenommen wird. Je höher der R-Quadrat-Wert ist, desto besser passt die Regressionsgleichung in die Daten.
Wie ist die Interpretation der Steigung und des Y-Abschnitts der Regressionsgleichung?
Die Steigung der Regressionsgleichung zeigt die Änderungsrate der abhängigen Variablen an, wenn sich die unabhängige Variable ändert. Der y-Schnittpunkt ist der Wert der abhängigen Variablen, wenn die unabhängige Variable gleich Null ist. Die Interpretation der Regressionsgleichung hängt vom Kontext ab, in dem sie verwendet wird.
Durch die Verwendung des Tools "Datenanalyse" in Excel können Sie die Regressionsgleichung leicht finden. Geben Sie einfach Ihre Daten in die entsprechenden Spalten ein und wählen Sie dann die Option Regressionsanalyse aus. Sie können dann die Ergebnisse interpretieren, um die Gleichung der Regressionslinie zu bestimmen. Mit den hilfreichen Funktionen von Excel war es noch nie einfacher, die Regressionsgleichung zu finden.




















