Wie berechnet man das Chi -Quadrat in Excel?

Suchen Sie eine schnelle und einfache Möglichkeit, das Chi -Quadrat in Excel zu berechnen? Wenn ja, sind Sie am richtigen Ort gekommen. In diesem Artikel führen wir Sie durch die Schritte der Berechnung des Chi -Quadrats in Microsoft Excel. Wir werden ein einfaches Beispiel angeben, um den Prozess zu veranschaulichen und Anleitung zur Interpretation der Ergebnisse zu geben. Am Ende dieses Artikels haben Sie das Vertrauen und das Wissen, das Chi -Quadrat in Excel zu berechnen. Fangen wir an!

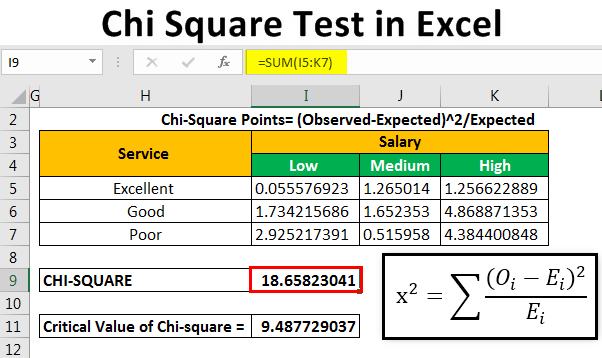
Einführung in die CHI -Quadratberechnung

Das Chi Square ist ein statistischer Test, mit dem beobachtete Daten mit erwarteten Daten verglichen werden. Es wird verwendet, um festzustellen, ob zwischen den beiden Datensätzen ein signifikanter Unterschied besteht. Das Chi -Quadrat kann auch verwendet werden, um Hypothesen über die Verteilung kategorischer Variablen zu testen. Dieser Artikel bietet einen Überblick über die Berechnung des Chi -Quadrats in Microsoft Excel.

Chi Square verstehen

Das Chi Square ist ein statistischer Test, mit dem beobachtete Daten mit erwarteten Daten verglichen werden. Der Test basiert auf der Chi-Quadrat-Statistik, die den Unterschied zwischen beobachteten und erwarteten Frequenzen in einer bestimmten Probe misst. Die Statistik wird berechnet, indem die erwartete Frequenz von der beobachteten Frequenz subtrahiert, dann das Ergebnis durch die erwartete Frequenz dividiert und das Ergebnis quadriert wird. Die Chi-Quadrat-Statistik wird dann mit dem kritischen Wert der Chi-Quadrat-Verteilung verglichen. Wenn der berechnete Wert größer als der kritische Wert ist, wird die Nullhypothese abgelehnt und der Unterschied zwischen den beobachteten und den erwarteten Frequenzen wird als statistisch signifikant angesehen.

Das Chi -Quadrat wird verwendet, um Hypothesen über die Verteilung kategorischer Variablen zu testen. Es wird verwendet, um festzustellen, ob es einen signifikanten Unterschied zwischen zwei Datensätzen gibt, z. B. die Ergebnisse einer Umfrage oder das Ergebnis eines Experiments. Der Test wird verwendet, um die beobachteten Häufigkeiten von zwei Variablen (z. von Produkt).

Berechnung des Chi -Quadrats in Excel

Das Berechnen des Chi -Quadrats in Microsoft Excel ist relativ einfach. Zu diesem Zweck müssen Sie die beobachteten und erwarteten Frequenzen in eine Excel-Tabelle eingeben und dann mit der Funktion der Chisq.dist die Chi-Quadrat-Statistik berechnen.

Die musk.distische Funktion nimmt drei Argumente an: die beobachtete Häufigkeit, die erwartete Häufigkeit und den Freiheitsgrad. Der Freiheitsgrad wird durch die Anzahl der Kategorien im Datensatz bestimmt. Wenn es beispielsweise zwei Kategorien gibt (z. B. männlich und weiblich), ist der Freiheitsgrad eins.

Schritte zur Berechnung des Chi -Quadrats in Excel

Der erste Schritt zur Berechnung des Chi -Quadrats in Excel besteht darin, die beobachteten und erwarteten Frequenzen in eine Excel -Tabelle einzugeben. Die beobachteten Frequenzen sollten in einer Spalte eingegeben werden, während die erwarteten Frequenzen in eine andere eingegeben werden sollten.

Der nächste Schritt besteht darin, die Funktion der Chisq.dist zu verwenden, um die Chi-Quadrat-Statistik zu berechnen. Diese Funktion nimmt drei Argumente an: die beobachtete Häufigkeit, die erwartete Häufigkeit und den Freiheitsgrad. Um die Funktion zu verwenden, geben Sie die beobachteten und erwarteten Frequenzen in die Funktion ein und geben Sie dann den Freiheitsgrad ein.

Die Ergebnisse interpretieren

Sobald die Funktion der Chisq.d-Funktion verwendet wurde, um die Chi-Quadrat-Statistik zu berechnen, kann das Ergebnis interpretiert werden. Wenn der berechnete Wert größer als der kritische Wert der Chi-Quadrat-Verteilung ist, wird die Nullhypothese abgelehnt, und der Unterschied zwischen den beobachteten und erwarteten Frequenzen gilt als statistisch signifikant.

Verwenden der Ergebnisse

Die Ergebnisse des Chi-Quadrat-Tests können auf verschiedene Weise verwendet werden. Wenn der Test beispielsweise verwendet wird, um die Ergebnisse einer Umfrage zu vergleichen, kann er verwendet werden, um festzustellen, ob ein signifikanter Unterschied zwischen den Präferenzen verschiedener Gruppen von Befragten besteht. Es kann auch verwendet werden, um Hypothesen über die Verteilung kategorieller Variablen zu testen, z. B. ob eine bestimmte Variable gleichmäßig auf eine Population verteilt ist.

Häufig gestellte Fragen

Was ist ein Chi -Quadrattest?

Ein Chi -Quadrat -Test ist ein statistischer Test, mit dem festgestellt wird, ob ein signifikanter Unterschied zwischen den erwarteten Frequenzen und den beobachteten Frequenzen in einer oder mehreren Kategorien besteht. Es wird auch verwendet, um Beziehungen zwischen zwei kategorialen Variablen zu testen. Der Chi -Quadrat -Test wird verwendet, um beobachtete Daten mit erwarteten Daten zu vergleichen, um festzustellen, ob ein signifikanter Unterschied zwischen ihnen besteht.

Was ist die Formel für einen Chi -Quadrat -Test?

Die Formel für einen CHI -Quadrattest lautet: x2 = σ, wobei O die beobachtete Frequenz und E die erwartete Frequenz ist. Die Zusammenfassung erfolgt in allen Kategorien. Das Ergebnis der Formel ist die Chi -Quadrat -Statistik, die dann verwendet werden kann, um die Signifikanz der Differenz zwischen den beobachteten und den erwarteten Frequenzen zu bestimmen.

Wie berechnet man das Chi -Quadrat in Excel?

Um die CHI -Quadratstatistik in Excel zu berechnen, müssen Sie die beobachteten und erwarteten Frequenzen in die entsprechenden Zellen eingeben. Geben Sie zunächst die beobachteten Frequenzen in die erste Spalte ein. Geben Sie dann die erwarteten Frequenzen in die zweite Spalte ein. Wählen Sie anschließend die beiden Datenspalten aus und wählen Sie die Option "Datenanalyse" auf der Registerkarte "Daten". Wählen Sie schließlich die Option "Chi-Quadrat-Test" und klicken Sie auf "OK". Die resultierende Chi -Quadrat -Statistik wird auf der Registerkarte "Ausgabe" angezeigt.

Welche Bedeutung hat die Chi Square -Statistik?

Die Signifikanz der CHI -Quadratstatistik wird durch Vergleich mit einem kritischen Wert aus der CHI -Quadratverteilungstabelle bestimmt. Wenn die berechnete Statistik größer als der kritische Wert ist, wird sie als signifikant angesehen und der Unterschied zwischen den beobachteten und den erwarteten Frequenzen ist nicht auf Zufall zurückzuführen. Wenn die berechnete Statistik geringer ist als der kritische Wert, wird sie als nicht signifikant angesehen und der Unterschied zwischen den beobachteten und den erwarteten Frequenzen wird als Zufall zurückzuführen.

Was sind die Annahmen eines Chi -Quadrattests?

Die Annahmen eines Chi -Quadrattests umfassen, dass die Daten kategorisch sein müssen, dass die erwarteten Frequenzen in jeder Kategorie größer als 5 sein sollten, dass die erwarteten Frequenzen mindestens 10% der Gesamtbeobachtungen betragen sollten und dass die Beobachtungen unabhängig sind.

Was sind die Einschränkungen eines Chi -Quadrattests?

Die Einschränkungen eines CHI -Quadrattests umfassen, dass er nicht für stark verzerrte Verteilungen geeignet ist, dass er gegenüber der Stichprobengröße empfindlich ist und nicht verwendet werden kann, um die Richtung der Beziehung zwischen zwei kategorialen Variablen zu bestimmen. Zusätzlich ist der CHI -Quadrattest nicht geeignet, um Beziehungen zwischen nicht kategorialen Variablen zu testen.

So berechnen Sie das Chi -Quadrat mit excel = chisq.test und = chisq.inv.rt

Zusammenfassend ist die Berechnung des Chi -Quadrats in Excel ein relativ einfacher Prozess. Mit nur wenigen Klicks können Sie die Chi -Quadrat -Statistik in Excel berechnen und sie verwenden, um Beziehungen zwischen zwei oder mehr Variablen zu analysieren. Unabhängig davon, ob Sie ein Student oder ein professioneller Forscher sind, ist es eine wichtige Fähigkeit, in Ihrer Datenanalyse -Toolbox zu verstehen, wie man das Chi -Square in Excel berechnet.