Wie berechnet man lineare Regression auf Excel?

Möchten Sie die lineare Regression auf Excel berechnen, wissen Sie aber nicht wie? Mach dir keine Sorgen - du bist am richtigen Ort gekommen! In diesem Artikel werden wir untersuchen, wie die lineare Regression auf Excel berechnet wird. Wir werden die notwendigen Formeln und Schritte diskutieren, die Sie unternehmen müssen, um die lineare Regression auf Excel zu berechnen. Am Ende dieses Artikels sind Sie auf dem besten Weg, dieses wertvolle Datenanalyse -Tool zu beherrschen. Also fangen wir an!

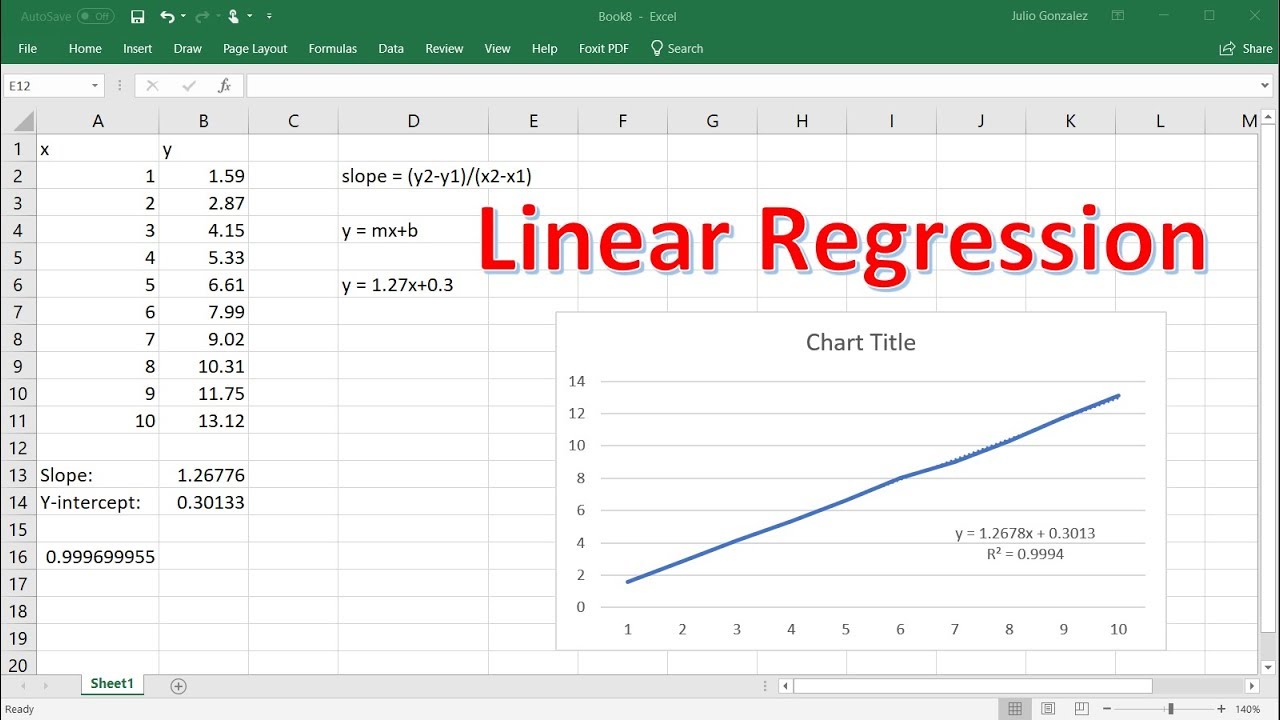
Einführung in die Berechnung der linearen Regression auf Excel

Lineare Regression ist ein leistungsstarkes Instrument zur Analyse von Daten und zum Verständnis von Beziehungen zwischen Variablen. Es wird oft verwendet, um Trends zu identifizieren und Vorhersagen zu treffen. Excel ist ein großartiges Werkzeug für diese Art der Analyse, da es problemlos lineare Regressionsgleichungen und grafische Darstellungen der Daten erzeugen kann. In diesem Artikel werden wir erklären, wie die lineare Regression auf Excel berechnet und die Ergebnisse interpretiert werden.

Schritte zur Berechnung der linearen Regression auf Excel

Schritt 1: Sammeln Sie die Daten

Der erste Schritt bei der Berechnung der linearen Regression auf Excel besteht darin, die von Ihnen verwendeten Daten zu sammeln. Diese Daten sollten in zwei Variablensätze organisiert werden: die unabhängige Variable, die untersucht wird, und die abhängige Variable, die vorhergesagt wird. Stellen Sie sicher, dass die Daten sauber sind und dass keine fehlenden Werte oder Ausreißer fehlen.

Schritt 2: Geben Sie die Daten in Excel ein

Sobald Sie die Daten gesammelt haben, müssen Sie sie in Excel eingeben. Dies kann erfolgen, indem entweder die Daten manuell eingeben oder sie in die Tabelle einfügen. Stellen Sie sicher, dass die Daten ordnungsgemäß organisiert sind, wobei die unabhängige Variable in der ersten Spalte und die abhängige Variable in der zweiten Spalte.

Schritt 3: Berechnen Sie die lineare Regressionsgleichung

Sobald die Daten in Excel eingegeben wurden, können Sie die lineare Regressionsgleichung berechnen. Klicken Sie dazu auf die Registerkarte "Daten" und wählen Sie in der Gruppe "Analyse" "Datenanalyse" aus. Wählen Sie in der Liste der Optionen "Regression" aus und klicken Sie auf "OK". Wählen Sie die Spalten mit den Daten aus und klicken Sie erneut auf "OK". Die lineare Regressionsgleichung wird im Abschnitt „Ausgabe“ angezeigt.

Interpretation der Ergebnisse der linearen Regression

Analyse der Koeffizienten

Die lineare Regressionsgleichung besteht aus Koeffizienten, die die Beziehung zwischen den unabhängigen und abhängigen Variablen darstellen. Der Koeffizient für die unabhängige Variable wird als „Steigung“ bezeichnet, während der Koeffizient für die abhängige Variable als „Abfang“ bezeichnet wird. Durch die Analyse dieser Koeffizienten können Sie Einblick in die Stärke und Richtung der Beziehung zwischen den beiden Variablen erhalten.

Berechnung des R-Quadratswerts

Der Wert R-Quadrat ist ein Maß dafür, wie gut die lineare Regressionsgleichung den Daten passt. Es ist eine Zahl zwischen 0 und 1, wobei höhere Werte auf eine bessere Passform hinweisen. Verwenden Sie zur Berechnung des R-Squared-Werts in Excel die Funktion „RSQ“, die zwei Argumente annimmt: die lineare Regressionsgleichung und den Datenbereich.

Abschluss

Lineare Regression ist ein leistungsstarkes Instrument zur Analyse von Daten und zum Verständnis der Beziehungen zwischen Variablen. Excel ist ein großartiges Instrument zur Berechnung der linearen Regressionsgleichungen und zur Analyse der Ergebnisse. Wenn Sie die in diesem Artikel beschriebenen Schritte befolgen, können Sie die linearen Regressionsgleichungen leicht berechnen und die Ergebnisse interpretieren.

Verwandte FAQ

1. Was ist eine lineare Regression?

Die lineare Regression ist eine mathematische Möglichkeit, die Beziehung zwischen zwei Variablen zu analysieren. Es wird verwendet, um die beste Anpassung für einen bestimmten Satz von Datenpunkten zu bestimmen, indem die Werte der beiden Variablen ermittelt werden, die die Summe ihres quadratischen Fehlers minimieren. Die Linie der besten Anpassung ist die Linie, die die Beziehung zwischen den beiden Variablen am besten beschreibt. Durch das Verständnis der Beziehung zwischen zwei Variablen kann man Vorhersagen über zukünftige Werte der beiden Variablen machen.

2. Was ist die Gleichung für die lineare Regression?

Die Gleichung für die lineare Regression lautet: y = mx + b, wobei y die abhängige Variable ist, m die Steigung der Linie, x ist die unabhängige Variable und B der y-Schnittpunkt.

3. Wie berechnen Sie die lineare Regression auf Excel?

Um die lineare Regression auf Excel zu berechnen, müssen Sie zwei Datenspalten haben. Sie müssen zunächst die Daten in die Tabelle eingeben. Anschließend müssen Sie die Datenpunkte auswählen, auf die Registerkarte "Einfügen einfügen" und dann das Diagramm "Streuung" auswählen. Dadurch wird ein Diagramm Ihrer Datenpunkte erstellt. Sobald das Diagramm erstellt wurde, müssen Sie auf die Registerkarte "Layout" klicken und dann auf "Trendline" klicken. Von hier aus können Sie der Tabelle eine lineare Regressionslinie hinzufügen.

4. Was sagt Ihnen der Wert R-Quadrat?

Der R-Quadrat-Wert zeigt, wie gut die Datenpunkte der besten Anpassung passen. Ein Wert von 1 zeigt an, dass die Datenpunkte perfekt zur Linie passen, während ein Wert von 0 angibt, dass die Datenpunkte nicht zur Leitung passen. Dieser Wert kann verwendet werden, um die Genauigkeit der Vorhersagen aus dem linearen Regressionsmodell zu bewerten.

5. Was sind die Annahmen der linearen Regression?

Die Annahmen der linearen Regression sind, dass die Datenpunkte einem linearen Muster folgen, dass es keine Multikollinearität gibt, dass die Residuen eine Normalverteilung haben und dass die Residuen unabhängig voneinander sind. Es ist wichtig, diese Annahmen bei der Verwendung einer linearen Regression zu berücksichtigen, da sie einen signifikanten Einfluss auf die Genauigkeit der vorgegebenen Vorhersagen haben können.

6. Was sind die Grenzen der linearen Regression?

Die Einschränkungen der linearen Regression umfassen die Tatsache, dass sie auf lineare Beziehungen zwischen zwei Variablen beschränkt ist, dass sie komplexe Beziehungen zwischen Variablen nicht berücksichtigen kann, und dass sie nicht verwendet werden kann, um Ergebnisse vorherzusagen, die außerhalb des Bereichs der verwendeten Datenpunkte liegen Erstellen Sie das Modell. Darüber hinaus berücksichtigt die lineare Regression keine Ausreißer, was erhebliche Auswirkungen auf die Genauigkeit der Vorhersagen haben kann.

Wenn Sie den angegebenen Schritten befolgen, können Sie die lineare Regression auf Excel schnell und einfach berechnen. Es ist ein nützliches Instrument, mit dem Sie Daten analysieren, Trends identifizieren und Vorhersagen treffen können. Mit diesem Wissen können Sie bessere Entscheidungen darüber treffen, wie Sie Ihre Daten für Prognose, Planung und andere Aufgaben am besten verwenden können. Probieren Sie es noch heute aus und sehen Sie die Kraft der linearen Regression in Aktion!