How to Calculate Linear Regression on Excel?

Are you looking to calculate linear regression on Excel but don’t know how? Don’t worry – you’ve come to the right place! In this article, we will be exploring how to calculate linear regression on Excel. We will discuss the necessary formulas and steps you need to take to calculate linear regression on Excel. By the end of this article, you will be well on your way to mastering this valuable data analysis tool. So, let’s get started!

Introduction to Calculating Linear Regression on Excel

Linear regression is a powerful tool for analyzing data and understanding relationships between variables. It is often used to identify trends and make predictions. Excel is a great tool for this type of analysis, as it can easily generate linear regression equations and graphical representations of the data. In this article, we’ll explain how to calculate linear regression on Excel and interpret the results.

Steps to Calculate Linear Regression on Excel

Step 1: Gather the Data

The first step in calculating linear regression on Excel is to gather the data that you’ll be using. This data should be organized into two sets of variables: the independent variable, which is the one that is being studied, and the dependent variable, which is the one that is being predicted. Make sure that the data is clean and that there are no missing values or outliers.

Step 2: Input the Data into Excel

Once you have gathered the data, you’ll need to input it into Excel. This can be done by either entering the data manually or by pasting it into the spreadsheet. Make sure that the data is properly organized, with the independent variable in the first column and the dependent variable in the second column.

Step 3: Calculate the Linear Regression Equation

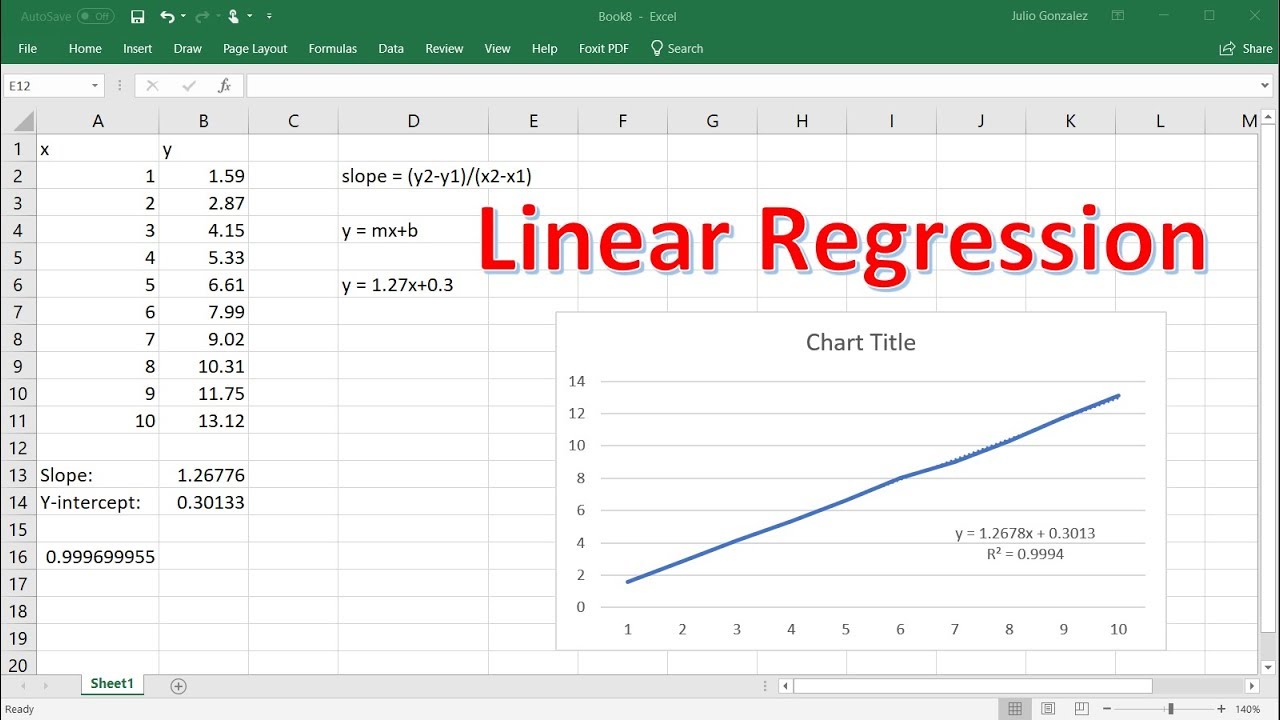
Once the data has been input into Excel, you can calculate the linear regression equation. To do this, click the “Data” tab and select “Data Analysis” from the “Analysis” group. Select “Regression” from the list of options and click “OK.” Select the columns containing the data and click “OK” again. The linear regression equation will be displayed in the “Output” section.

Interpreting the Results of the Linear Regression

Analyzing the Coefficients

The linear regression equation is composed of coefficients, which represent the relationship between the independent and dependent variables. The coefficient for the independent variable is known as the “slope,” while the coefficient for the dependent variable is known as the “intercept.” By analyzing these coefficients, you can gain insight into the strength and direction of the relationship between the two variables.

Calculating the R-Squared Value

The R-squared value is a measure of how well the linear regression equation fits the data. It is a number between 0 and 1, with higher values indicating a better fit. To calculate the R-squared value in Excel, use the “RSQ” function, which takes two arguments: the linear regression equation and the range of data.

Conclusion

Linear regression is a powerful tool for analyzing data and understanding the relationships between variables. Excel is a great tool for calculating linear regression equations and analyzing the results. By following the steps outlined in this article, you can easily calculate linear regression equations and interpret the results.

Related Faq

1. What is Linear Regression?

Linear Regression is a mathematical way to analyze the relationship between two variables. It is used to determine the line of best fit for a given set of data points by finding the values of the two variables that minimize the sum of their squared error. The line of best fit is the line that best describes the relationship between the two variables. By understanding the relationship between two variables, one can make predictions about future values of the two variables.

2. What is the equation for Linear Regression?

The equation for Linear Regression is: y = mx + b, where y is the dependent variable, m is the slope of the line, x is the independent variable, and b is the y-intercept.

3. How do you calculate Linear Regression on Excel?

To calculate Linear Regression on Excel, you need to have two columns of data. You first need to enter the data into the spreadsheet. Then, you need to select the data points, click the “Insert” tab, and then choose the “Scatter” chart. This will create a graph of your data points. Once the graph is created, you need to click the “Layout” tab and then click “Trendline”. From here, you can choose to add a linear regression line to the chart.

4. What does the R-Squared value tell you?

The R-Squared value tells you how well the data points fit the line of best fit. A value of 1 indicates that the data points perfectly fit the line, while a value of 0 indicates that the data points do not fit the line. This value can be used to assess the accuracy of the predictions made from the linear regression model.

5. What are the assumptions of Linear Regression?

The assumptions of Linear Regression are that the data points follow a linear pattern, that there is no multicollinearity, that the residuals have a normal distribution, and that the residuals are independent of each other. It is important to consider these assumptions when using Linear Regression as they can have a significant impact on the accuracy of the predictions made.

6. What are the limitations of Linear Regression?

The limitations of Linear Regression include the fact that it is limited to linear relationships between two variables, that it cannot account for complex relationships between variables, and that it cannot be used to predict outcomes that are outside of the range of the data points used to create the model. Additionally, Linear Regression does not account for outliers, which can have a significant impact on the accuracy of the predictions.

By following the steps provided, you can quickly and easily calculate linear regression on Excel. It is a useful tool to help you analyze data, identify trends, and make predictions. With this knowledge, you can make better decisions about how to best use your data for forecasting, planning, and other tasks. Try it out today and see the power of linear regression in action!